Proofs of a Trembling-hand and not a Trembling-hand Perfect Equilibrium in Selten’s Example

Reinhard Selten, famous for introducing the trembling-hand perfect equilibrium into the world of game theory provided a numerical example of why his refinement concept of Nash equilibrium was relevant (Selten & Bielefeld, 1988). In his example, he showed that the Nash equilibrium $(R, \rho, A)$ is a trembling-hand perfect equilibrium and stated that the Nash equilibrium $(L, \rho, B)$ was not. When reading through his analysis and proof of why this was the case, I was confused about the latter.

In this blog post, for my understanding of this equilibrium concept, I try to provide an alternative proof for why $(R, \rho, A)$ is a Trembling-hand perfect equilibrium (different than the proof that Selten and Börgers provides) and a, hopefully, clearer proof by contradiction for why $(L, \rho, B)$ is not a Trembling-hand perfect equilibrium.

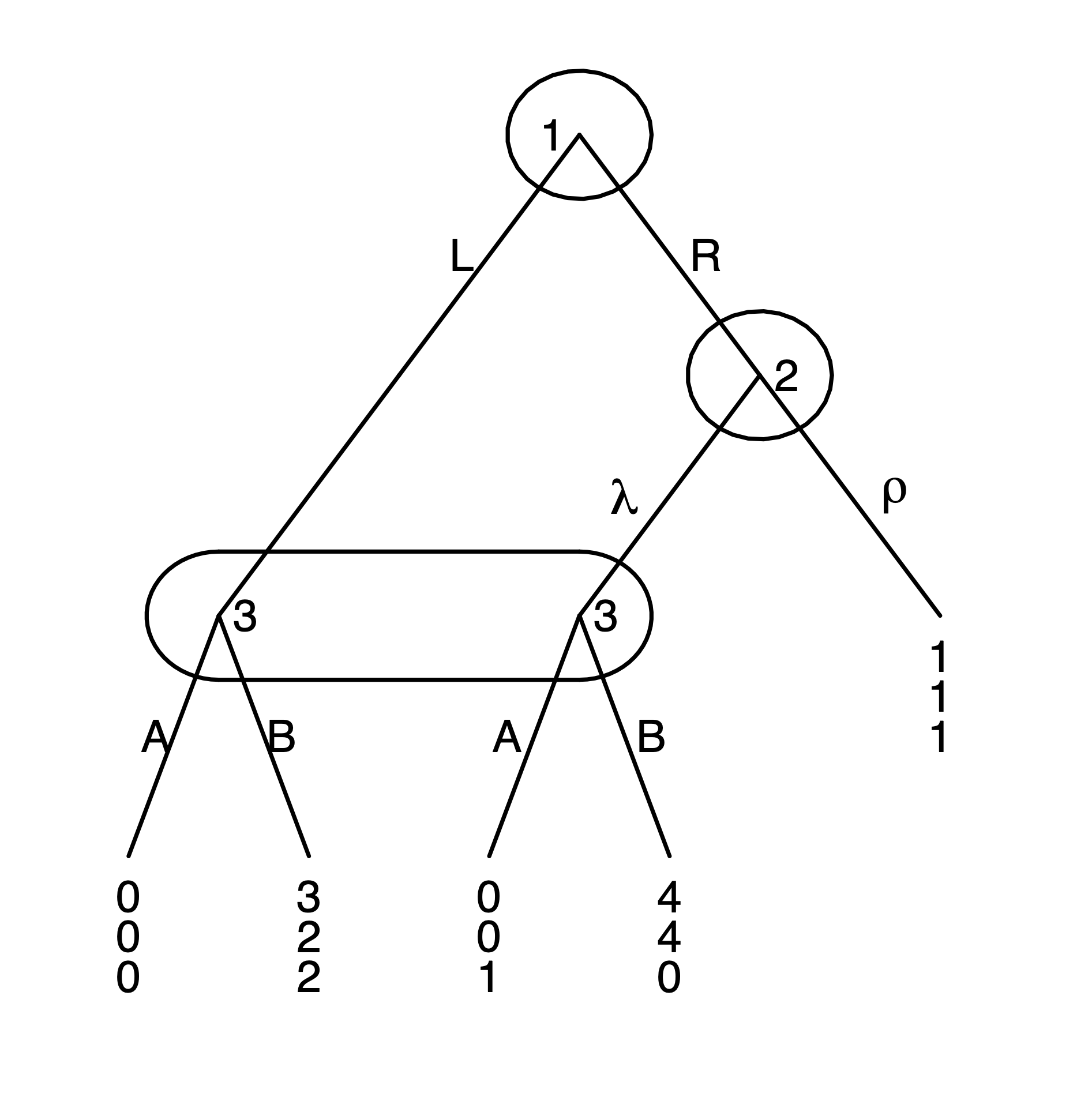
A Trembling-hand and not a Trembling-hand Perfect Equilibrium

I provide the definition of Trembling-hand Perfect Equilibrium in order to show Selten’s two important results. Note that this definition extends the definition provided in Börger’s notes (that is I list an extra condition for Trembling-hand Perfect Equilibrium) but is consistent with Selten’s definition.

$\textbf{Definition. Trembling-hand Perfect Equilibrium}$

A list of behavior strategies $b^{*}=\left(b_{1}^{*}, b_{2}^{*}, \ldots, b_{n}^{*}\right)$ is a (trembling hand) perfect equilibrium if there exists a sequence of lists of perturbations

$\left(\delta^{k}\right)_{k \in \mathbb{N}}=\left(\delta_{1}^{k}, \delta_{2}^{k}, \ldots, \delta_{n}^{k}\right)_{k \in \mathbb{N}}$

and a sequence of lists of behavior strategies

$\left(b^{k}\right)_{k \in \mathbb{N}}=\left(b_{1}^{k}, b_{2}^{k}, \ldots, b_{n}^{k}\right)_{k \in \mathbb{N}}$

(note that each player’s behavior strategies may depend on the perturbation) such that for every player $i \in I$,

(1) for every information set $V_{i}^{j}$ of player $i$, and every action $a_{i} \in A_{i}\left(V_{i}^{j}\right), \lim _{k \rightarrow \infty} \delta_{i}^{k}\left(a_{i}\right)=0$, (higher $k$ modeling less tremble and lower $k$ modeling more tremble)
(2) for every $k \in \mathbb{N}, b^{k}$ is a Nash equilibrium of $\Gamma\left(\delta^{k}\right)$,
(3) $\lim _{k \rightarrow \infty} b_{i}^{k}=b_{i}^{*}$, and
(4) for every $k \in \mathbb{N}$, information set $V_{i}^{j}$ of player $i$, and $a_{i} \in A_{i}\left(V_{i}^{j}\right), \delta_{i}^{k}\left(a_{i}\right) \leq b_{i}^{k}\left(a_{i}\right) \leq 1-\sum_{a_{i}^{\prime} \in A_{i}\left(v_{i}^{j}\right) \setminus \left\{a_{i}\right\}} \delta_{i}^{k}\left(a_{i}^{\prime}\right)$ (there is a lower and upper bound for the behavior strategy determined by the perturbation since we require there to be a small amount of error for each action).

$\textbf{Proposition.}$ $(R, \rho, A)$ is a Trembling-hand perfect equilibrium.

$\textit{Proof.}$ For the behavior strategy $(R, \rho, A)$ to be a Trembling-hand perfect equilibrium, there must exist a sequence of lists of perturbations and behavior strategies such that the conditions listed in the definition are satisfied. Let $\epsilon \in(0,0.25)$ and consider the following sequence of behavior strategies along with the perturbations. Suppose

$b(A)=1-\epsilon^{k}, b(B)=\epsilon^{k}, b(\lambda)=\epsilon^{k}, b(\rho)=1-\epsilon^{k}, b(L)=\frac{\epsilon^{k}}{2+\epsilon^{k}}, b(R)=1-\frac{\epsilon^{k}}{2+\epsilon^{k}},$

$\delta(B)=\delta(\lambda)=\delta(A)=\delta(\rho)=\delta(R)=\epsilon^{k}$, and $\delta(L)=\frac{\epsilon^{k}}{2+\epsilon^{k}}$. Conditions (1) and (3) are satisfied in this case. Now consider condition (4). For $b(L)$, we must have that

$\delta(L) \leq \frac{\epsilon^{k}}{2+\epsilon^{k}} \leq 1-\delta(R).$

For $b(\lambda)$, we must have that

$\delta(\lambda) \leq \epsilon^{k} \leq 1-\delta(\rho).$

For $b(A)$, we must have that

$\delta(A) \leq 1-\epsilon^{k} \leq 1-\delta(B).$

Note that I don’t check $b(R)$ or the others since the constraint $\delta(R) \leq b(R)=1-b(L) \leq 1-$ $\delta(L)$ is equivalent to the constraint for $b(L)$. Hence, after checking the constraints above, condition (4) is satisfied. Now I check condition (2). The following is true for all $k \in \mathbb{N}$. For player $1, R$ is preferred to $L$ if

$\begin{gathered} 3 b^{k}(B) \leq b^{k}(\rho)+4\left(1-b^{k}(\rho)\right) b^{k}(B) \\ \Leftrightarrow \\ 3 \epsilon^{k} \leq 1-\epsilon^{k}+4\left(\epsilon^{k}\right)^{2}. \end{gathered}$

For player $2, \rho$ is preferred to $\lambda$ if

$\begin{gathered} 4 b^{k}(B) \leq 1 \\ \Leftrightarrow \\ \epsilon^{k} \leq \frac{1}{4}. \end{gathered}$

For player 3, $A$ is preferred to $B$ if

$\begin{gathered} 2\left(1-b^{k}(R)\right) \leq b^{k}(R)\left(1-b^{k}(\rho)\right) \\ \Leftrightarrow \\ 2\left(\frac{\epsilon^{k}}{2+\epsilon^{k}}\right) \leq \left(1-\frac{\epsilon^{k}}{2+\epsilon^{k}}\right) \epsilon^{k}. \end{gathered}$

Hence, condition (2) is satisfied.

$\textbf{Proposition.}$ $(L, \rho, B)$ is not a Trembling-hand perfect equilibrium.

$\textit{Proof.}$ Suppose for the sake of contradiction that $(L, \rho, B)$ is a perfect equilibrium. Hence, there is a sequence of behavior strategies $b^{k}(B)$ for player 3 such that player 2 prefers $\rho$ over $\lambda$. Since condition (2) is satisfied, we must have that for player 2, for all $k, 1>4 b^{k}(B)$ (i.e. the expected value of player 2 choosing $\rho$ is greater than the expected value of player 2 choosing $\lambda$). Note that this argument is valid because there is no Nash equilibrium where player 2 chooses $\lambda$ with probability 1. Further note that we cannot have $b^{k}(B)=\frac{1}{4}$, since that would violate condition (3). Hence, player 3’s best response must be $b^{k}(B)<\frac{1}{4}$. But this then violates condition (3) which requires that $\lim _{k \rightarrow \infty} b^{k}(B)=1$. Hence, we have arrived at a contradiction and $(L, \rho, B)$ cannot be a Trembling-hand perfect equilibrium.

References

1. Selten, R., & Bielefeld, R. S. (1988). Reexamination of the perfectness concept for equilibrium points in extensive games. Springer.