Minimizing Waiting Time Given Lists of Resources

Finding the optimal schedule of resources such that the total time agents must wait between using the resources is minimized turns out to be a linear programming problem that uses elements of graph theory. In this article, I describe agents as students and resources as classes that they must take, but the model can be generalized to include many other situations.

Model

There are $k$ courses, $c_1, \ldots, c_k$, and $n$ students at a school. The set of all courses is denoted $C=\left\{c_1, \ldots, c_k\right\}$. The school is open for $t \in \mathbb{R}_{+}$ time.

Each student $i=1, \ldots, n$ has a set of courses that they would like to take, denoted as $K_i$. The number of courses that each student can take is less than $k$. Hence, the set $K_i$ is a strict subset of $C$, i.e. $K_i \subset C$. The duration of each course $c_i$ is $t_i \in \mathbb{R}_{+}$ time.

The school manager chooses the starting $x_i \in[0, t)$ and ending $y_i \in(0, t]$ times of each course $c_i \in C$ such that $y_i-x_i=t_i$. Let the starting and ending times of each course be ordered by the sequence of intervals $J:=\left(\left[x_i, y_i\right]\right)_{i=1}^k$.

$\textbf{Definition. Concurrent Courses}$

Suppose $Q$ is the set of students that are taking a course $c_i \in C$. A course $c_i$ can occur at the same time as another course $c_j \neq c_i$ if no student in $Q$ is taking $c_j$, i.e. $c_j \notin \bigcup_{i \in Q} K_i$.

Let $\mu$ be defined to be the Lebesgue measure. For each student $i$, set of courses $K_i$, and the starting and ending times of each course ordered by the sequence of intervals, $J$, define the time interval that the student spends in class as the union of disjoint time intervals $\mathcal{J}_i\left(K_i, J\right):=\bigcup_{c_q \in K_i} J_q$. Let the total time student $i$ spends at school be the interval $L_i\left(K_i, J\right):=\left[\min \left(\mathcal{J}_i\left(K_i, J\right)\right), \max \left(\mathcal{J}_i\left(K_i, J\right)\right)\right]$. For each student $i$, the time lost function is the length of the complement of the time interval that the student spends in class defined as

$\Phi_i\left(K_i, J\right):=\mu\left(\left\{x \in L_i\left(K_i J\right) \mid x \notin \mathcal{J}_i\left(K_i, J\right)\right\}\right).$

$\textbf{Definition. Optimality}$

Starting and ending times of courses $J^*$ is optimal if

$\bigcap_{c_q \in K_i} J_q^*=\emptyset \tag{1}$

for every student $i=1, \ldots, n$ (the sequence of time intervals is feasible) and

$\sum_{i=1}^n \Phi_i\left(K_i, J^*\right) \leq \sum_{i=1}^n \Phi_i\left(K_i, J^{\prime}\right) \tag{2}$

for any $J^{\prime} \in\left\{\left(\left[x_i, y_i\right]\right)_{i=1}^k \mid \forall i, x_i \in \mathbb{R}_{\geq 0}\right.$ and $y_i-x_i=t_i$ and $\left.\bigcap_{c_q \in K_i} J_q^{\prime}=\emptyset\right\}$ (no feasible alternative sequence of time intervals is strictly less than the optimal schedule).

An Algorithm to Find the Optimal Schedule

I now describe an algorithm to find the optimal schedule, if it exists. The optimal schedule may not exist depending on how long the school is open, $t$, and the duration of each course $t_i$. As you will see, the solution depends on a linear programming problem, which may or may not have a solution.

First, I provide some important definitions that the algorithm will use. Most of these definitions can be found in graph theory textbooks such as (Balakrishnan & Ranganathan, 2012).

$\textbf{Definition. Intersection Graphs}$

Let $\mathcal{F}:=\left\{S_1, \ldots, S_p\right\}$ be a family of sets. The intersection graph of $\mathcal{F}$ consists of vertices $v_i$ for each set $S_i$ and a set of edges $\left\{\left\{v_i, v_j\right\} \mid i \neq j, S_i \cap S_j \neq \emptyset\right\}$. If $S_i$ is an interval, then the intersection graph is called an interval graph.

$\textbf{Definition. Subgraph}$

A graph $H=(W, F)$ is a subgraph of a graph $G=(V, E)$ if $W \subseteq V$ and $F \subseteq E$. A subgraph $H$ of a graph $G=(V, E)$ is generated if $F=\{\{x, y\} \in E \mid x, y \in W\}$ (i.e. $H$ includes all edges in $E$ whose vertices are in $W$).

$\textbf{Definition. Clique}$

A graph is complete if, for any two vertices, there is an edge. A clique in a graph $G=(V, E)$ is a complete subgraph. A clique is dominant if it is not contained in any larger clique. An ordering of dominant cliques $\left(\omega_1, \ldots, \omega_n\right)$ is called consecutive if for any three indices $\alpha, \beta, \gamma$ such that $\alpha<\beta<\gamma$, if a vertex $a \in V$ belongs to both $\omega_\alpha$ and $\omega_\gamma$, then $a$ belongs to $\omega_\beta$.

Consider the algorithm as follows.

1. Create an undirected graph denoted by $G:=(C, E)$ which consists of $C$, a set of vertices representing courses, and $E$, a set of edges such that an edge connects course $c_i$ with $c_j$ if and only if course $c_i$ can occur at the same time as another course $c_j$.

2. For each generated subgraph of $G$ that is an interval graph, $S$, and ordering of dominant cliques $\omega_1, \ldots, \omega_u$ of $S$ that is consecutive, let a length of time of $\omega_i$ be denoted as $D_i$ and let $J$ be constructed using $D_i$ and the ordering of dominant cliques. Then solve the linear program by selecting $D_i \geq 0$ to $\operatorname{minimize} \sum_{i=1}^n \Phi_i\left(K_i, J\right)$ such that $\sum_{i=1}^u D_i \leq t$ and the time of each course $c_i$ is $t_i$ in $J$.

Note that for step 2, there are theorems that simplify the search space. For example, a graph is an interval graph if and only if it is a rigid circuit graph and it has no asteroidal triple, see (Lekkeikerker & Boland, 1962).

If the number of courses, $k$, is large, the second step of the algorithm may not be feasible. In such a case, a solution might be to first use the algorithm above to generate optimal starting and ending times of courses (given example lists of courses that are small and $k$ is small) and then create a neural network to learn the underlying pattern to predict optimal schedules for larger $k$. This might be a potential path to research further.

An Application of the Algorithm

Suppose that there are six courses and five students. The list of courses that each student would like to take is $K_1=\left\{c_1, c_3, c_4\right\}, K_2=\left\{c_1, c_2\right\}, K_3=\left\{c_1, c_4\right\}, K_4=\left\{c_2, c_5\right\}$, and $K_5=\left\{c_4, c_5, c_6\right\}$. Suppose the school is open for $t=$ 3 hours, and each course requires one hour.

An iteration of the algorithm might result in the following computation. First, the undirected graph $(C, E)$ is constructed as follows.

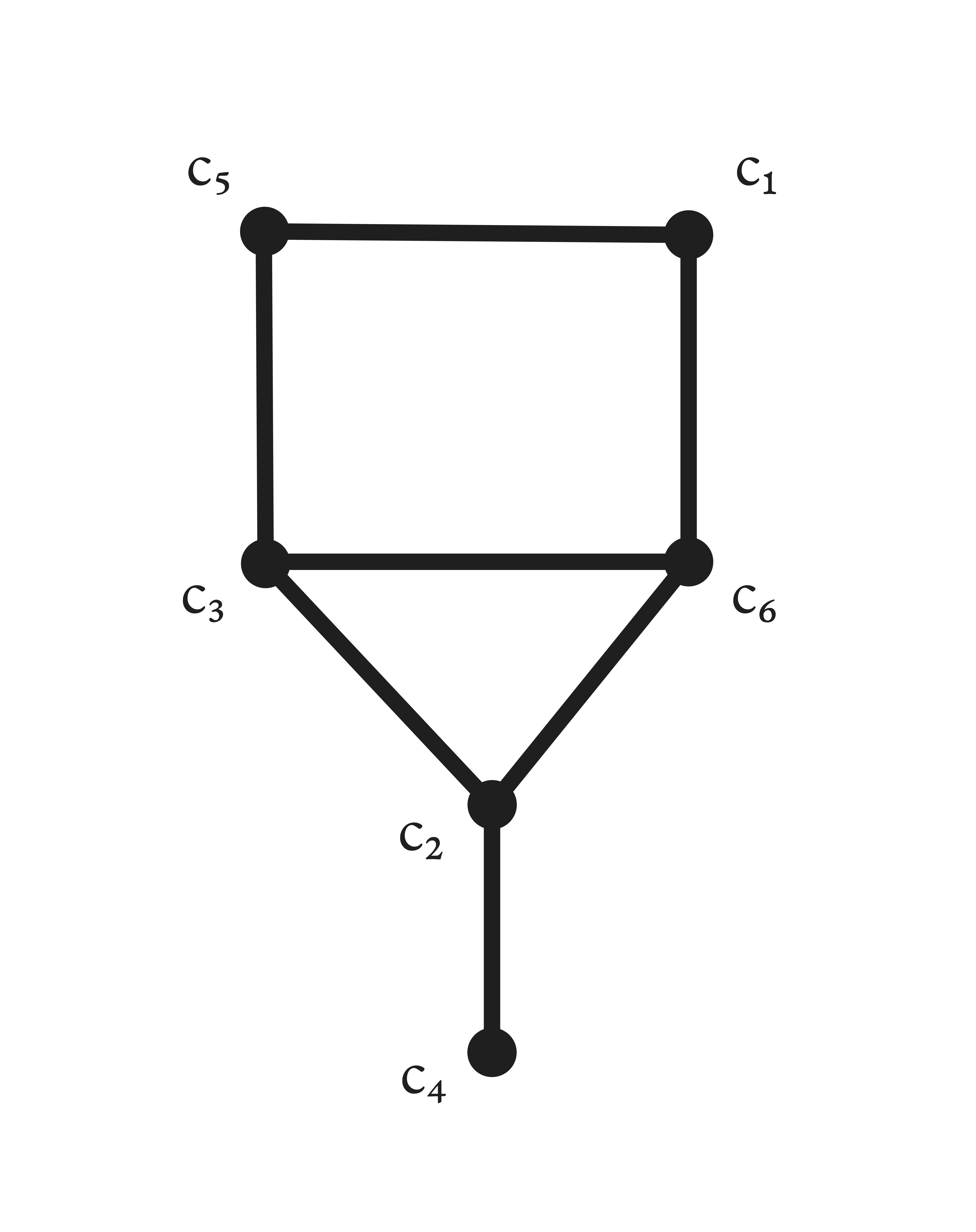
Next, a generated subgraph that is an interval graph might remove the edge connecting $c_1$ to $c_6$. An ordering of dominant cliques $\omega_1, \ldots, \omega_4$ of the generated subgraph that is consecutive is $\omega_1=\left\{c_1, c_5\right\}, \omega_2=\left\{c_5, c_3\right\}, \omega_3=\left\{c_3, c_6, c_2\right\}$, and $\omega_4=\left\{c_2, c_4\right\}$. The linear programming problem is then constructed as

$\operatorname{minimize} 2 D_2+D_3$

such that $D_1+D_2+D_3+D_4 \leq 3, D_1 \geq 1, D_1+D_2 \geq 1, D_2+D_3 \geq 1, D_3 \geq 1, D_3+D_4 \geq 1$, and $D_4 \geq 1$ and $D_i \geq 0$ for all $i=1, \ldots, 4$. The solution to the minimization problem for this generated subgraph is $D_1=1, D_2=0, D_3=1$, and $D_4=1$. The interval graph representing the starting and ending times of each course would be as follows.

Under this schedule, the only person who must wait is student 3, who would like to take $c_1$ and $c_4$.

References

1. Balakrishnan, R., & Ranganathan, K. (2012). A textbook of graph theory. Springer Science & Business Media.
2. Lekkeikerker, C., & Boland, J. (1962). Representation of a finite graph by a set of intervals on the real line. Fundamenta Mathematicae, 51(1), 45–64.