Greedy Algorithm and the Priority Mechanism

In the matroid theory literature, the greedy algorithm finds the independent set in the matroid with the maximum weight. This type of algorithm was extended in (Roth et al., 2005) to find a matching among patients that is Pareto efficient and matches as many high-priority patients as possible. In this article, I give an example of how the greedy algorithm determines which acyclic part of the graph has the maximum aggregate weight and give an example to show how the greedy algorithm is extended into the priority algorithm.

Generally, there are many situations in which the greedy algorithm can be used to find some optimal solution. I provide examples of how this algorithm finds solutions to different problems in order to further understand how it might be generalized. Perhaps a way of generalizing how the greedy algorithm results in optimal solutions is to find similarities between the examples I provide. I do not want to make this article extremely complicated, so I avoid this route and only present the examples.

Application of the Greedy Algorithm to Acyclic Graphs

Before presenting an example of how the greedy algorithm is traditionally used, I will provide some important definitions.

$\textbf{Definition. Matroid}$
A matroid is a pair $M=(E, \mathcal{J})$, where $E$ is a finite set, and $\mathcal{J} \subseteq 2^E$ is a collection of subsets of $E$, called the independent sets, satisfying the following properties.

1. $\mathcal{J}$ contains at least one set.
2. If $J_1 \in \mathcal{J}$ and $J \subseteq J_1$, then $J \in \mathcal{J}$.
3. If $J_1, J_2 \in \mathcal{J}$ and $\left|J_1\right|>\left|J_2\right|$, there exists an element $e \in J_1 \setminus J_2$ such that $J_2 \cup\{e\} \in \mathcal{J}$.

$\textbf{Algorithm. The Greedy Algorithm For Acyclic Graphs}$
Given a matroid $M=(E, \mathcal{J})$ with a weight function $w(e)$ for each $e \in E$, the greedy algorithm finds an independent set $J \in \mathcal{J}$ of maximum weight.

1. Initialize $J=\emptyset$, the set containing elements with the maximum weight.
2. Order the elements of $E$ so that $w\left(e_i\right) \geq w\left(e_{i+1}\right)$.
3. At iteration $i$, if $\left\{e_i\right\} \cup J \in \mathcal{J}$, append $\left\{e_i\right\}$ to $J$ and consider the next iteration.

Now consider the weighted graph as follows, where the vertices are labeled $v_i$ for all $i=1, \ldots, 4$ and the edges labeled $a, \ldots, d$. Let the weights be $w_a:=w(a)=2, w_b:=w(b)=3, w_c:=w(c)=1$, and $w_d:=w(d)=4$. A matroid that we can consider resulting from this graph consists of the edges of the graph $\{a, \ldots, d\}$ and all acyclic subgraphs. We could also substitute acyclic subgraphs with cycles or combinations of edges up to some cardinality to obtain a matroid. While there are probably some applications of such matroids, I do not explore them further here.

The greedy algorithm orders the weights as $\left(w_d, w_b, w_a, w_c\right)$ and produces the acyclic graph $c, d, b$, yielding a total weight of 8. There is no other acyclic subgraph that has a higher total weight.

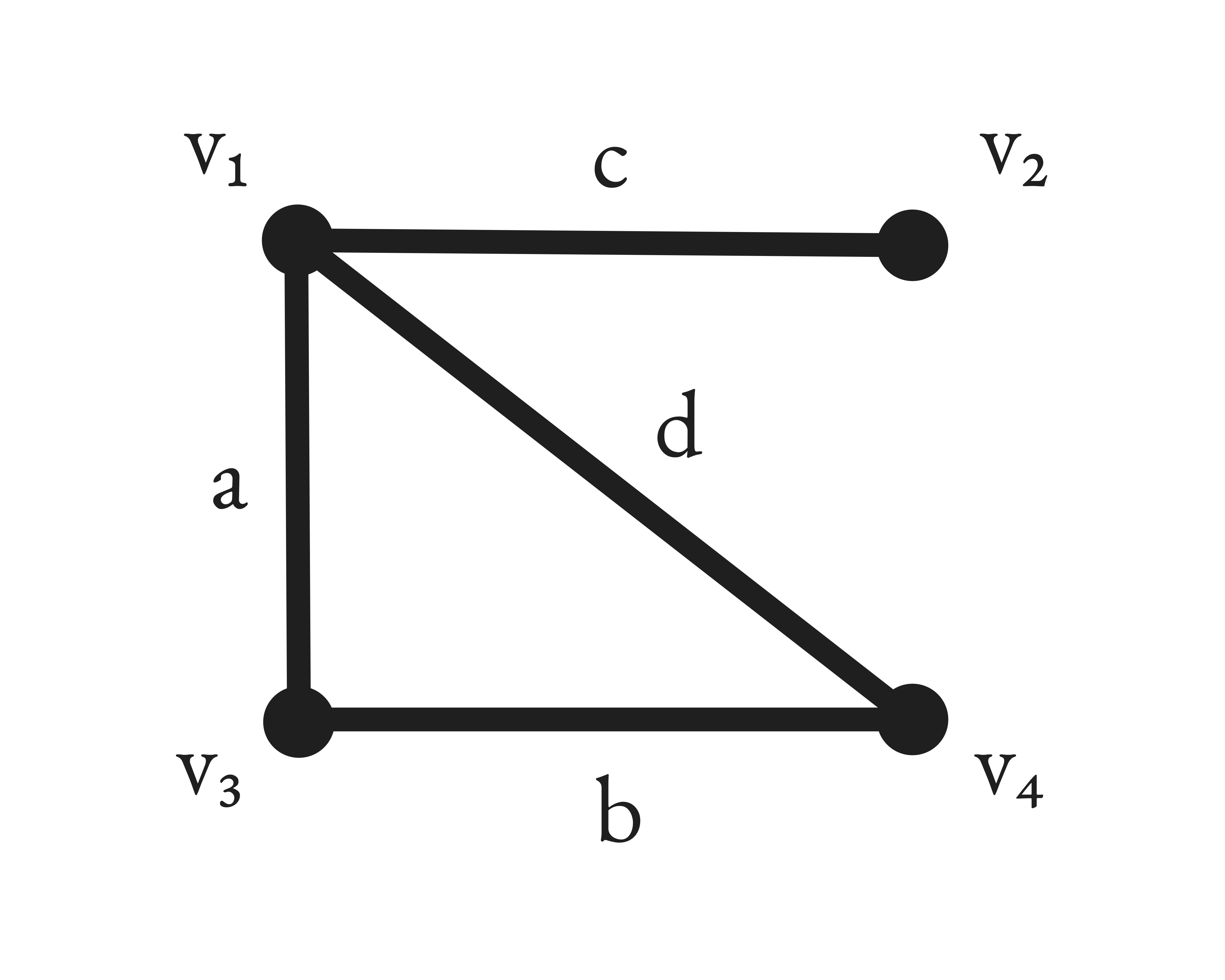
The general idea behind the greedy algorithm is that it greedily selects the component that will contribute the most toward the goal as long as it fits the constraints of the problem. If the component does not fit the constraint, then it should be eliminated. The result of greedily selecting components in each iteration results in a global optimum.

As you will see in the section below, the priority mechanism is a greedy algorithm with a similar pattern. Although the greedy algorithm for acyclic graphs cannot be directly applied, an adjustment can be made. Instead of selecting one edge at a time to construct the independent set with the maximum weight, consider all maximal independent sets and filter these sets by considering the highest-weighted items. This process of filtration yields the independent set with the maximum weight.

Application of the Greedy Algorithm to Match High-Priority Patients

In this section, I present the definition of the priority algorithm, which can be found in the paper (Roth et al., 2005), and I provide an example. But first, I review some important notation.

There are $n$ number of patients contained in the set $N=\{1, \ldots, n\}$. Pairs $i, j$ are mutually compatible if $j$ has a compatible donor for the patient of $i$ and $i$ has a compatible donor for the patient of $j$, that is, $k_j \in K_i$ and $k_i \in K_j$. A mutual compatibility matrix $R=\left[r_{i, j}\right]_{i, j \in N}$ is defined as for any $i, j \in N$,

$r_{i, j}=\left\{\begin{array}{ll}1 & \text { if } i \text { and } j \text { are mutually compatible } \\ 0 & \text { otherwise }\end{array}.\right.$

A compatibility graph consisting of mutually compatible patients can be defined as $G=(N, E)$, where $E$ is the set of edges connecting mutually compatible patients.

A matching of patients $\mu$ is a set that contains pairs of mutually compatible patients that are matched with one another and patients matched with themselves. Patient $p_i \in N$ is matched with patient $p_j \in N$ in the matching $\mu$ if and only if $\mu=\left\{p_i p_j\right\}$. In this model, cycles of matched patients are not considered. Hence, it cannot be the case that $\mu=\left\{p_i p_j p_k\right\}$ for some $p_i, p_j, p_k \in N$. Note that a matching can contain multiple elements, and patients who are matched with themselves are of the form $p_i p_i$ (e.g. $\mu=\left\{p_1 p_2, p_3 p_4, p_5 p_5\right\}$). A priority ordering $\left(p_1, \ldots, p_n\right)$ among the patients orders each patient $p_i$ from 1 being the highest priority to $n$ being the lowest. Each patient has a distinct integer representing their priority.

$\textbf{Algorithm. The Priority Mechanism}$
Given any compatibility graph $G$ and priority ordering among the patients, the priority algorithm finds a maximal matching.

1. Let $\mathcal{E}^0$ be the set of maximal matchings
2. For priority ordering $\left(p_1, \ldots, p_i, \ldots, p_n\right)$ and $1 \leq i \leq n$, let $\mathcal{E}^i \subseteq \mathcal{E}^{i-1}$ be defined as

$\mathcal{E}^i=\left\{\begin{array}{ll} \left\{\mu \in \mathcal{E}^{i-1} \mid p_i p_i \notin \mu\right\} & \text { if } \exists \mu \in \mathcal{E}^{i-1} \text { s.t. } p_i p_i \notin \mu \\ \mathcal{E}^{i-1} & \text { otherwise } \end{array}.\right.$

Consider the following graph with vertices that represent patients and edges connecting two patients if and only if they are compatible with one another. A patient is matched with themselves only if he cannot be matched with any others. Suppose that the priorities of patients are represented as the weights of vertices. $w\left(v_1\right)=1, w\left(v_2\right)=4, w\left(v_3\right)=3, w\left(v_4\right)=2$, and $w\left(v_5\right)=5$. Hence, patient 1 has the highest priority, and patient 5 has the lowest priority. The priority ordering is $(1,4,3,2,5)$. This, along with the subsets of patients such that a matching contains these patients, defines a matroid. We can then apply the greedy algorithm to find the independent set of maximum weight. Note that if the independent sets were matchings of the compatibility graph instead of the patients contained by some matching, then this would not be a matroid.

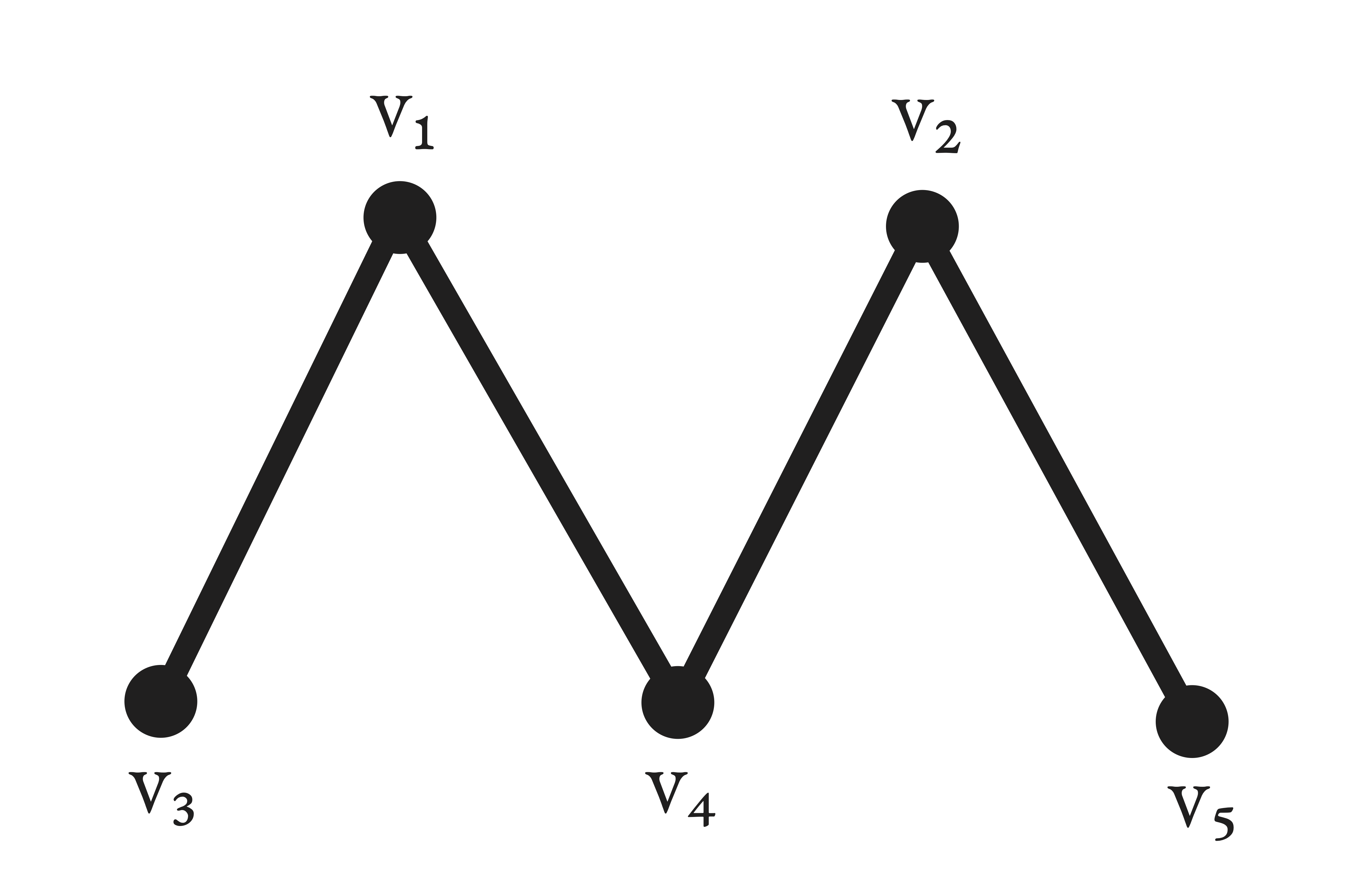
In the first iteration, potential matchings that contain the patient with the highest priority, patient 1, are $\{13,24,55\}$, $\{13,25,44\}$, and $\{14,25,33\}$. In the second iteration, potential matchings that contain patient 4 from the previous potential matching such that patient 4 is not matched with himself are $\{14,25,33\}$ and $\{13,24,55\}$. This process continues until only the matching $\{13,24,55\}$ is left. This matching includes as many high-priority patients as possible. In the graph above, by the Gallai–Edmonds decomposition theorem, there will only be 1 patient matched with himself for any priority ordering. Given the specific priority ordering $(1,4,3,2,5)$, the patient matched with himself (i.e. $55$) is the one with the lowest priority. However, it is generally not true that unmatched patients will always have lower priority than matched patients.

References

1. Roth, A. E., Sönmez, T., & Ünver, M. U. (2005). Pairwise kidney exchange. Journal of Economic Theory, 125(2), 151–188.